I den här publikationen kommer vi att överväga vad den Gaussiska metoden är, varför den behövs och vad dess princip är. Vi kommer också att visa med ett praktiskt exempel hur metoden kan tillämpas för att lösa ett system av linjära ekvationer.
Beskrivning av Gaussmetoden
Gauss metod är den klassiska metoden för sekventiell eliminering av variabler som används för att lösa. Den är uppkallad efter den tyske matematikern Carl Friedrich Gauss (1777-1885).
Men låt oss först komma ihåg att SLAU kan:
- ha en enda lösning;
- har ett oändligt antal lösningar;
- vara inkompatibla, dvs inte ha några lösningar.
Praktiska fördelar
Gaussmetoden är ett utmärkt sätt att lösa en SLAE som innehåller mer än tre linjära ekvationer, såväl som system som inte är kvadratiska.
Principen för Gauss-metoden
Metoden inkluderar följande steg:
- rakt – den förstärkta matrisen som motsvarar ekvationssystemet reduceras över raderna till den övre triangulära (stegvisa) formen, dvs under huvuddiagonalen bör endast element vara lika med noll.
- tillbaka – i den resulterande matrisen är elementen ovanför huvuddiagonalen också nollställda (nedre triangulär vy).
Exempel på SLAE-lösning
Låt oss lösa systemet med linjära ekvationer nedan med Gauss-metoden.
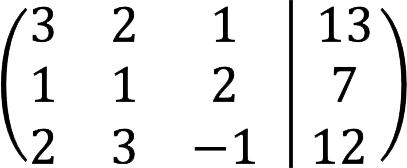
Lösning
1. Till att börja med presenterar vi SLAE i form av en utökad matris.
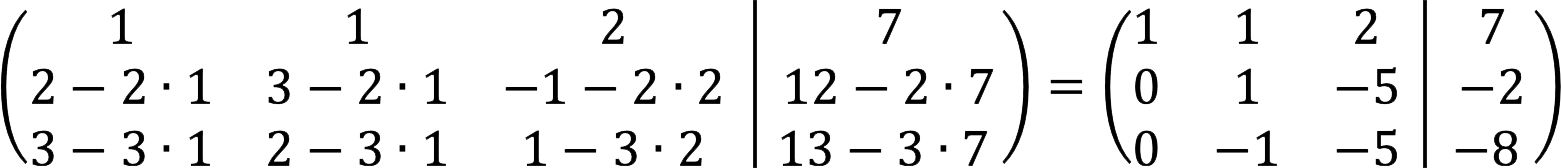
2. Nu är vår uppgift att återställa alla element under huvuddiagonalen. Ytterligare åtgärder beror på den specifika matrisen, nedan kommer vi att beskriva de som gäller för vårt fall. Först byter vi raderna och placerar därmed deras första element i stigande ordning.
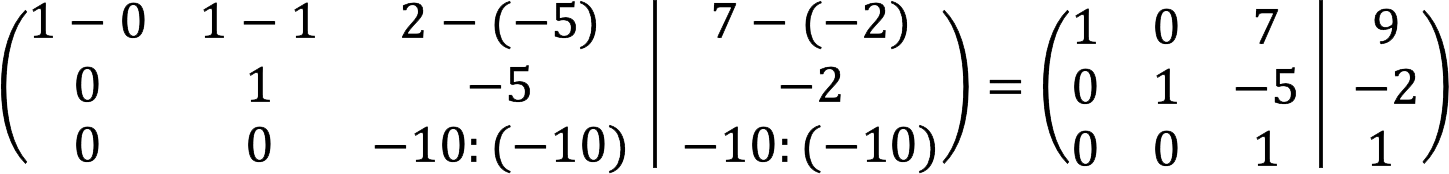
3. Subtrahera från den andra raden två gånger den första, och från den tredje – tredubbla den första.
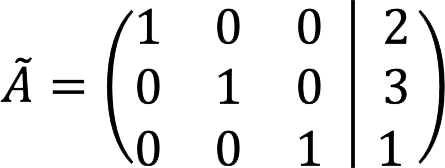
4. Lägg till den andra raden till den tredje raden.
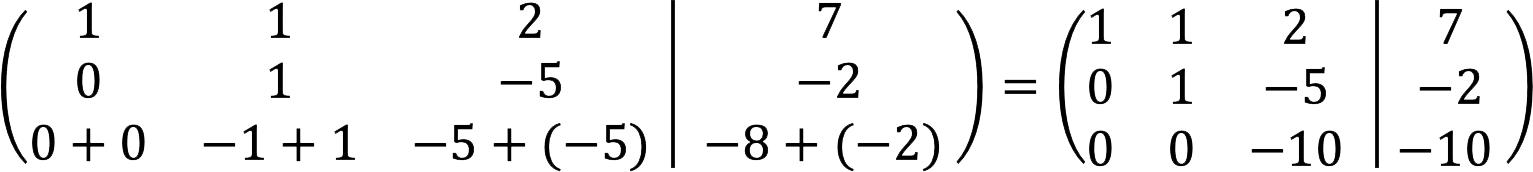
5. Subtrahera den andra raden från den första raden, och dividera samtidigt den tredje raden med -10.
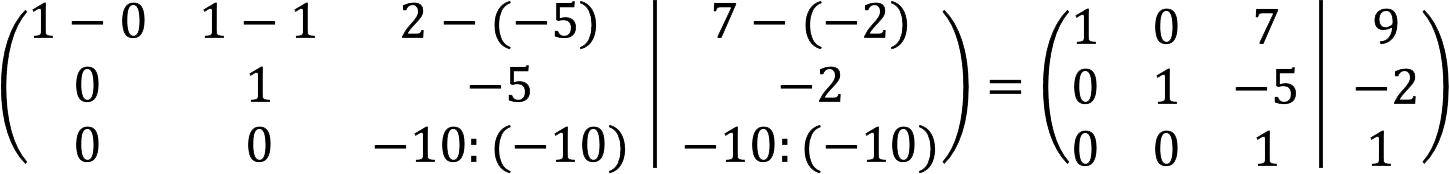
6. Den första etappen är klar. Nu måste vi få nollelementen ovanför huvuddiagonalen. För att göra detta, subtrahera den tredje multiplicerad med 7 från den första raden och lägg till den tredje multiplicerad med 5 till den andra.
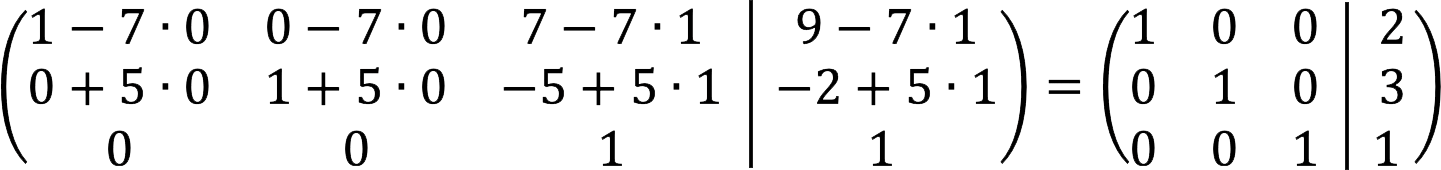
7. Den slutliga expanderade matrisen ser ut så här:
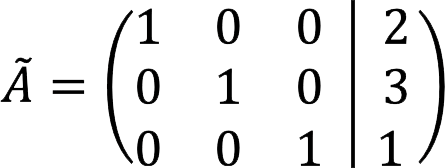
8. Det motsvarar ekvationssystemet:
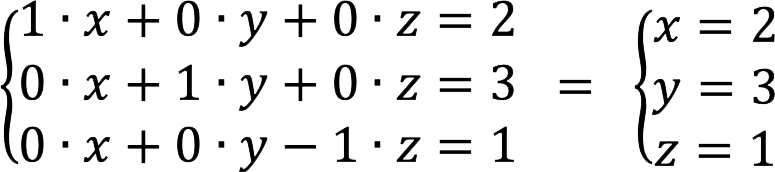
Svar: root SLAU: x = 2, y = 3, z = 1.










